Determining Uncertainties in Measured Values
Uncertainties in measured values may be due to instrumental uncertainty or to procedural uncertainty.
Instrumental UncertaintyInstrumental uncertainty is the uncertainty in the measurement due to the limit of precision in the instrument.
- For most glassware in chemistry, like graduated cylinders or beakers, the uncertainty is printed on the instrument.
- For most analogue scales, the uncertainty is estimated as half the smallest division, although for some thermometers with large markings, it is possible to estimate to the nearest third of the marking.
- For standard metersticks and rulers, the uncertainty is 1 mm.
- For digital instruments, the uncertainty is the smallest division. For example if your voltmeter reads 3.47 V, then the uncertainty would be 0.01 V.
- For computer probes, the most appropriate way to estimate the uncertainty is to take data for several seconds in an unchanging situation (for example place a temperature probe in a glass of water and take readings for several seconds). Then do a statistical analysis of the data and use the standard deviation as the instrument uncertainty.
Procedural uncertaintyProcedural uncertainty refers to the variation in results when repeating the same measurement several times. It is due to the inability to completely control all factors affecting an experiment.
This is why we take three trials and find the average whenever possible. The simplest way to get a rough estimate of the procedural uncertainty is to take half of the range of one set of trials. We usually use the largest, typical range of all your sets of three trials.
Example: Absolute UncertaintyLooking at the example below, we see that the set of trials for 210 Hz has the largest range of all the sets of trials. The range in these three trials is (38.4 - 38.1 cm) = 0.3 cm. The uncertainty is 0.5*0.3 = 0.15 cm ~ 0.2 cm since we round all estimated uncertainty to 1 significant figure.
Frequency and Distance from the End of the Tube to the Water Level (First Harmonic)
Frequency
(±1 Hz)Distance from End of Tube to Water Level (±0.2 cm)
Trial 1
Trial 2
Trial 3
450
17.0
16.9
16.9
390
19.6
19.9
19.7
330
23.5
23.7
23.5
270
29.3
29.4
29.4
210
38.4
38.2
38.1
150
54.5
54.4
54.4
Table 1: The frequency emitted by the frequency generator and the point of resonance from the water level to the end of the tube. The uncertainties of the frequency and the distance are the instrumental uncertainty of the frequency generator, and the ruler respectively.
The Frequency and the Mean Distance from the End of the Tube to the Water Level (First Harmonic)
Average Distance From End of Tube to Water Level (±0.2 cm)
450
16.9
390
19.7
330
23.6
270
29.4
210
38.2
150
54.4
Table 2: The frequency and the average distance from the end of the tube to the water surface. The uncertainty of the average distance was taken from half the largest range of all trials.
Example: Relative UncertaintyIn some cases, using the absolute range of the trials is not the best way estimate the uncertainty. In cases where the range of the trials increases significantly as the averages increase, it is appropriate to use the largest percent range of the three trials.
Looking at the example below, we see that half the range of the three trials increases from 0.05 for the 100 ml trials all the way to 1.65 (~2) for the 600 ml trials. To estimate an uncertainty of ± 2 m/s for all the data would imply that the uncertainty is greater than the speed for the 100 ml trial. This is not an accurate representation of the data.
It is better in this case to look at the percentage uncertainty. Taking half the range and dividing by the average gives us the percent uncertainty. This ranges from 4 % to 6 % for the different sets of trails. It is greatest, at 6 %, for the 400 ml set of trials. This is a better way of estimating a realistic uncertainty in this case.
Table 1: Volume of water in a water rocket and its maximum speed
Volume
(±1 ml)Maximum speed of the water rocket (m/s) (± 6 %)
Trial 1
Trial 2
Trial 3
Average
100
1.0 0.9 1.0 1.0 200
4.4 4.1 4.5 4.3 300
8.5 8.6 8.0 8.4 400
12.7 14.2 12.6 13.2 500
17.9 17.2 19.1 18.1 600
28.3 26.3 29.6 28.1 Table 1: The volume of water in the rocket and the maximum velocity of the rocket for each trial and the averages. The uncertainty of the volume was the instrumental uncertainty of the graduated cylinder. The uncertainty of the speed is the greatest percentage range of the trials.
Determining Uncertainties in Calculated Values
When you are calculating a value, like speed, it is important to determine how many significant figures you know in your value, and how large your uncertainty is. An uncertainty is a rough estimate of how far off a value might be, so it should be rounded to one significant figure.
The calculated data value should then be rounded off to the decimal place where the uncertainty starts. If the uncertainty starts in the hundredths place, you obviously cannot have any valid information about the value of the thousandths place.
Example: Finding the speed of a snail, with the associated uncertainty in the calculated speed.Say you wanted to determine the speed of a snail. You had measured that it had traveled a distance of 127 ± 1 mm in a time of 30 ± 1 seconds. The speed is calculated as distance/time, or 4.2333 mm/s.
The uncertainty in the speed is calculated as +/- 0.158 mm/s. (See below for how to calculate the uncertainty.) If the uncertainty starts in the tenths place, then we cannot have any sure knowledge of anything less than that, so we should drop all digits past where the uncertainty starts. The uncertainty should be rounded to one significant figure, or ± 0.2. The value of the speed should be rounded to match the decimal place where the uncertainty starts, or 4.2.
The speed of the snail is correctly reported as 4.2 ± 0.2 mm/s. To report a value for speed to the hundredths place (4.23) is to claim you know something you are uncertain of. That is foolish at best and dangerous at worst.
Scientists must report the uncertainty in all measured and calculated values in order to ensure their honesty and to let the reader judge the strength and validity of their results.
It is often difficult to correctly calculate and present uncertainties. Three methods of doing this are presented below.
The first method is the easiest to do and understand. It is not elegant, and takes a bit more space to show, but it is a straight-forward and clear method of calculating and presenting uncertainties.
The other two ways are more elegant, but students often get confused and make mistakes when using them.
You may choose the method that you feel is best for you.
Examples Here are some examples of how to calculate and present uncertainties using the first two techniques below.
1. The Direct Method to Calculate and Present Uncertainties
The simplest way to calculate and present uncertainties is as an extension of your sample calculations. Start by showing your sample calculations using your actual values for the data. Then re-calculate the answer using the uncertainties to give the highest and lowest possible values of the data.
Here is a simple example of how to do this, using the case of measuring the velocity of a snail above. The snail traveled a distance of 127 ± 1 mm in a time of 30 ± 1 s.
Sample Calculations for the Velocity of a Snail
Actual Value for Velocity: v = d/t = 127 mm / 30 s = 4.23 mm/s
Highest Possible Value for Velocity: v = (127+1)mm / (30-1)s = 4.41 mm/s **
Lowest Possible Value for Velocity: v = (127-1)mm / (30+1)s = 4.06 mm/sUncertainty = (4.41 mm/s - 4.06 mm/s)/2 = (0.35 mm/s)/2 = 0.175 mm/s = 0.2 mm/s
Velocity of Snail = 4.2 ± 0.2 mm/s
**Note that the lowest possible value in the denominator gives the highest possible value of the result.
Here is another example of how to calculate the uncertainty in the kinetic energy of a cart. The velocity of a cart was measured as 2.3 ± 0.2 m/s and the mass of the cart was measured as 0.853 ± 0.001 kg. The equation for kinetic energy is K= (1/2)mv2.
Sample Calculations for the Kinetic Energy of the Cart
Actual Value for Kinetic Energy: K = (1/2)mv2 = (1/2) * 0.853 kg * (2.3 m/s)2 = 2.26 J
Highest Possible Value for K: K = (1/2) * (0.853+0.001) kg * (2.3+0.2 m/s)2 = 2.67 J
Lowest Possible Value for K: K = (1/2) * (0.853-0.001) kg * (2.3-0.2 m/s)2 = 1.88 JUncertainty = (2.67 J - 1.88 J)/2 = (0.79 J)/2 = 0.395 J = 0.4 J
Kinetic Energy of Cart = 2.3 ± 0.4 J
2. Mathematical Techniques for Calculating Uncertainties
The following is an explanation of how the uncertainties of calculated values are determined, using the concepts of absolute and relative uncertainty. This method gives the same results as the method above. If you are good in math, you may find this method more elegant, but it is easy to get confused using this method.
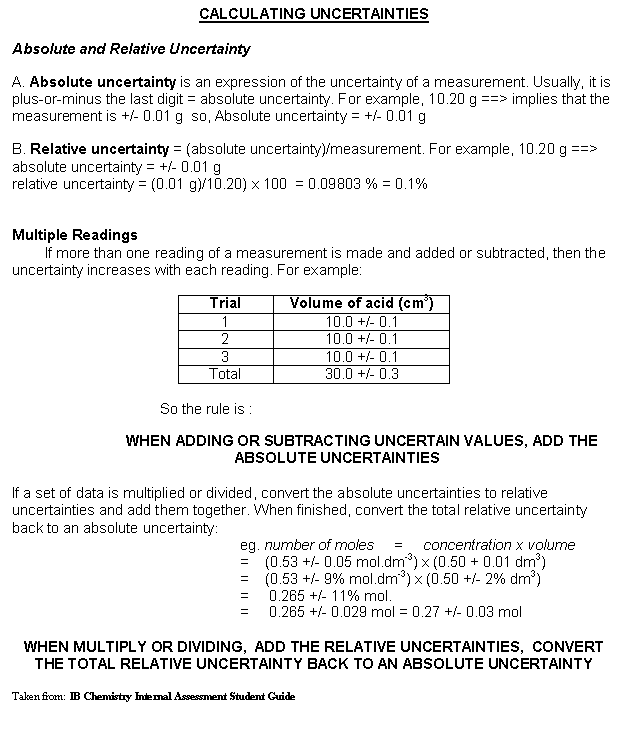 |
3. Calculating Uncertainties Using Excel
The following tables provide examples and templates that can be used to calculate the uncertainties in your analyzed data. The templates are not to be used to calculate all your results. They are to be used to calculate the uncertainty for one representative data point.
For each type of calculation, an example from a real lab is given, then a link to a template for you to use. Open the template in Excel, then just fill in your raw data values with high and low uncertainties in the appropriate spaces and the uncertainty in the result will be calculated. The resulting tables can be inserted into the Sample Calculations section of your lab report to show how the uncertainties in your calculated values were determined.
You will always need to "Format Cells" to modify the number of decimal places to fit your values. Remember, the uncertainty should be rounded to 1 significant figure, and the value should be rounded to match the uncertainty.
Types of Uncertainty Calculations
- Adding two data values
- Subtracting two data values
- Multiplying two data values
- Dividing two data values
- Multiplying a data value by a constant
- Calculating the inverse of a data value
- Using complex equations with two data values
- Manipulating a data value with complex functions for graphing
- Multiplying and dividing three data values
1. Adding Two Data Values
A student measures the distance from the floor to the top of the table. (D1 = 0.853 ± 0.002 m) Then, separately, measures the distance from the top of the table to the top of a ramp. (D2 = 0.372 ± 0.001 m) The uncertainty in the total distance, floor to top of ramp will be calculated as shown (D3 = 1.225 ± 0.003 m).
D1 (m) (± 0.002) |
D2 (m) (± 0.001) |
D3 (m) |
Calculated Uncert in D3 |
|
Uncert |
0.855 |
0.373 |
1.228 |
|
Value |
0.853 |
0.372 |
1.225 |
0.003 |
Uncert |
0.851 |
0.371 |
1.222 |
Here is a blank Template to use if you need to calculate the uncertainty for adding two data points, (A+B=C). Open it as an Excel file, then just fill in your values and you've got it! If you need to add more than two data points, just copy B column, insert it as an extra column, and adjust the equations for C. Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
2. Subtracting Two Data Values
A student measures the length of a potato core before soaking it in salt water. (L1 = 6.7 ± 0.05 cm) Then the student measures the length of the core after it has been soaked in salt water. (L2 = 6.2 ± 0.05 cm). The uncertainty in the change in length of the core is calculated as △L = -0.5 ± 0.1 cm.
L1 (cm) (± 0.05) |
L2 (cm) (± 0.05) |
△L (cm) |
Calculated Uncert in △L |
|
Uncert |
6.75 |
6.15 |
-0.6 |
|
Value |
6.70 |
6.20 |
-0.5 |
-0.1 |
Uncert |
6.65 |
6.25 |
-0.4 |
Here is a blank Template to use if you need to calculate the uncertainty for subtracting two data points, (B-A=C). Open it as an Excel file, then just fill in your values and you've got it! Note that since you are subtracting, the low and high values of uncert must be flipped for B compared to A. Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
3. Multiplying two data values
A student measures the mass (m = 1.08 kg ± 0.01 kg and velocity (v = 2.31 ± 0.06 m/s) of a cart and needs to calculate the uncertainty in the momentum (momentum = mass * velocity = 2.49 ± 0.09 kg m/s )
m (kg) ( ± 0.01) |
v (m/s) ( ± 0.06) |
momentum (kg*m/s) |
Calc Uncert in momentum |
|
Uncert |
1.09 |
2.37 |
2.58 |
|
Value |
1.08 |
2.31 |
2.49 |
0.09 |
Uncert |
1.07 |
2.25 |
2.41 |
Here is a blank Template to use if you need to calculate the uncertainty for multiplying two data points, (A*B=C). Open it as an Excel file, then just fill in your values and you've got it! Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
4. Dividing two data values
A student measures the time for a measured volume of hydrogen gas to be produced in order to calculate the rate of production of the gas. The volume of the gas is measured to be 15.0 ± 0.1 ml, and it takes a time of 57 ± 2 s. The calculated uncertainty in the rate of production of the gas is R = 0.26 ± 0.01 ml/s.
Volume (ml) ( ± 0.1) |
time (s) ( ± 2) |
Rate of Prod. (ml/s) |
Calc Uncert in Rate |
|
Uncert |
15.1 |
55 |
0.27 |
|
Value |
15.0 |
57 |
0.26 |
0.01 |
Uncert |
14.9 |
59 |
0.25 |
Here is a blank Template to use if you need to calculate the uncertainty for multiplying two data points, (A*B=C). Open it as an Excel file, then just fill in your values and you've got it! Note that since you are dividing, the low and high values of uncert must be flipped for B compared to A. Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
5. Multiplying a data value by a constant
A student measures the time for a pendulum to complete 5 swings as 7.4 ± 0.1 s. To convert the time for 5 swings into the periond (time for 1 swing), the student must multiply his data by 0.2 (1/5 = 0.2). The calculated uncertainy in the period of the pendulum is T = 1.48 ± 0.02 s.
Time for 5 swings (s) ( ± 0.1) |
Constant to multiply |
Time for 1 swing (s) |
Calc Uncert in Time |
|
Uncert |
7.5 |
0.2 |
1.50 |
|
Value |
7.4 |
1.48 |
0.02 |
|
Uncert |
7.3 |
1.46 |
Here is a blank Template to use if you need to calculate the uncertainty for multiplying a data value by a constant, (A*k=B). Open it as an Excel file, then just fill in your values and you've got it! Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
6. Calculating the inverse of a data value
A student measures the time for leaf discs to rise in water when exposed to sunlight as 17 ± 3 s. The rate of photosynthesis (R) can be represented as 1/(time to rise). The uncertainty in the rate is calculated as R = 0.06 ± 0.01 s-1
| time (s) ( ± 3) | Rate of Photosynth. (s-1) | Calc Uncert in Rate | |
| Uncert | 14 | 0.07 | |
| Value | 17 | 0.06 | 0.01 |
| Uncert | 20 | 0.05 |
Here is a blank Template to use if you need to calculate the uncertainty in the inverse of a data value. Open it as an Excel file, then just fill in your values and you've got it! Note that since you are dividing, the low and high values of uncert in the data are flipped. Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
7. Using complex equations with two data values
A student measures the mass (m = 1.08 ± 0.01 kg and velocity (v = 2.31 ± 0.06 m/s) of a cart and needs to calculate the uncertainty in the kinetic energy of the cart as KE = 0.5 * m * v2 = 2.9 ± 0.2 J
m (kg) ( +/- 0.01) |
v (m/s) ( +/- 0.06) |
KE (J) |
Calc Uncert in KE |
|
Uncert |
1.09 |
2.37 |
3.1 |
|
Value |
1.08 |
2.31 |
2.9 |
0.2 |
Uncert |
1.07 |
2.25 |
2.7 |
Here is a blank Template to use if you need to calculate the uncertainty in the combination of two data points with a complex multiplication, (for example 0.5*A*B2=C). Open it as an Excel file, then just fill in your values and you've got it! Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
8. Manipulating a data value with complex functions for graphing
A student measures the frequency of oscillation of a mass on a spring. It is predicted that the frequency is proportional to the inverse root of the mass. The student measures the mass (m = .350 ± 0.001 kg) and calculates the uncertainty in the inverse root of the mass as √(1/m) = 1.690 ± 0.002 kg-1/2.
mass (kg) (± .001) |
√(1/mass) (kg-1/2 ) |
Calc Uncert in √(1/m) |
|
Uncert |
0.349 |
1.693 |
|
Value |
0.350 |
1.690 |
0.002 |
Uncert |
0.351 |
1.688 |
Here is a blank Template to use if you need to calculate the uncertainty in the complex manipulation of a data point, in this example B = √(1/A). Open it as an Excel file, then just fill in your values and you've got it! If you need to determine the uncertainty for other manipulations, for example B = A2, B = √A, B = sin(A), B = log(A), B = ln(A), just change the equations for B in the three cells appropriately, and you've got it. Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.
9. Multiplying and dividing three data values
In some cases you need to combine three data values in a complex multiplication/division function. In a chemistry titration, the volume and concentration of the titrant and the volume of the analyte are known. These data are used to calculate the concentration of the analyte. For example, if 25.3 ± 0.1 ml of 0.100 ± 0.001 M NaOH is titrated with 20.00 ± 0.06 ml of HCL of unknown concentration. The equation: Conc HCl = (Vol NaOH * Conc NaOH)/(Vol HCl) is used. The uncert of the Conc HCl is calculated to be Conc HCL = 0.127 ± 0.002 M
Vol NaOH (ml) ( ± 0.1) |
Conc NaOH (M) ( ± 0.001) |
Vol HCl (ml) ( ± 0.06) |
Conc HCl (M) |
Calc Uncert in Conc |
|
Uncert |
25.4 |
0.101 |
19.94 |
0.129 |
|
Value |
25.3 |
0.100 |
20.00 |
0.127 |
0.002 |
Uncert |
25.2 |
0.099 |
20.06 |
0.124 |
Here is a blank Template to use if you need to calculate the uncertainty in multiplying/dividing three data points, (A*B)/C = D. Open it as an Excel file, then just fill in your values and you've got it! If you are doing a different manipulation with three data points, just change the equation for D in the three cells appropriately. Just be sure to adjust the position of the high and low uncert for each column to match whether it is in the numerator or the denominator. Don't forget to "Format Cells" to select the appropriate number of significant figures based on your uncertainty, then copy the table into the Sample Calcs section of your lab report.