The virtual image formed behind a convex lens when the object is inside the focal length is the enlarged image seen in a magnifying glass. A virtual image cannot be displayed on a screen and is consequently more difficult to locate than its real counterpart. The preferred method, is known as the method of no parallax.
An image and a marker both appear in the field of view.
The marker is seen above the lens. The image of the skewer is seen (in focus) in the lens. The marker and the image stay together when the observer moves from side to side only if they are in the same place.
Hint: when dodging backwards and forwards the images move slightly with respect to each other if the adjustment is not quite right. When the marker is moved to just the right place the movement stops. The impression created is of the two being suddenly locked together - the system goes 'dead'. Click the images repeatedly to see the effect.
Note: The image and the marker are behind the lens. It is not possible to focus the camera on the image, the marker, and the lens at the same time. The photographs at right have the lens and the marker out of focus. Altering the camera setting to bring the lens into focus blurs the image and further blurs the marker.
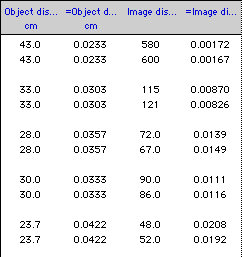
Six identical* convex lenses were selected. The lenses were placed in holders on tables, with an object (short sate skewer) and a clamp stand used as a marker.
The markers were positioned so that there was no parallax between the image of the skewer in the lens and the marker above the lens. The marker was then moved until it was just possible to tell that the marker was misplaced. The range was written down as maximum and minimum values of the image distance, v. The data is listed in table 1 below.
*The lenses were all from the same manufacturer, all of the same appearance, and all had the same focal length (46.0 cm to within ±1 mm), measured by focusing the image of a distant light on a wall.
Table 1

The data is plotted in the sequence of graphs at right. The possible errors are represented by possible maximum and minimum points, calculated for the graphs showing reciprocals.
Graph 1 shows an automatic curve fit of the function ...
The value of A is the focal length of the lens.
Graph 1a and Graph 1b are manual line fits showing that the focal length has been determined to within ±.1.cm.
Graph 2 is an automatic straight line fit to showing that the slope is +1 as expected within errors and that the focal length (the reciprocal of the intercept) is 46 cm.
Graph 2a and Graph 2b are extreme manual fits within the errors shown. The focal length has been determined by this method to within ± 5 cm and the slope of the line is +1 to within ± 0.08.
The thin lens formula ...
... has been shown to apply in this instance within the errors.
Errors
The method of no parallax is more difficult to apply than locating a real image with a screen, but, with care, the data confirms the thin lens formula as expected.
Moving the marker until parallax is just noticeable between the image and the marker allows maximum and minimum values for the image distance to be entered in table 1.
Note: Graphical Analysis was used to display the data since Logger Pro 3.0 did not allow connecting lines to be inserted between maximum and minimum points or the fitting of a curve with a repeated constant in the relationship. The double entry system gives the correct propagation of errors to the calculation of reciprocals. The second objection has been corrected in Logger Pro 3.4 but not the first. Ed.
Evaluation
Setting several lenses on the tables at the same time made the measurements easier, in the sense that the settings could all be checked at the same time by several people. The objection is of course, that the lenses were not, strictly speaking, identical. No variations due to using different lenses were apparent in this limited set of measurements.
Graph 1 has a good range of data points. In particular, the points near six meters on the image distance axis were very important for establishing the error in the focal length from this graph. In future, more points in the 2-10 meter range for image distances would greatly improve the reliability of student generated data, and this demonstration would also have benefited from more points in this region.
1 A condom filled with brine is a spherical convex lens with a positive focal length when submerged in tap water. An enlarged virtual image of the distant face is seen in the lens which acts as a magnifying glass. The focal length of the lens can be found by using the lens maker's formula, with the known radii and refractive indices.
A second condom is filled with tap water and submerged in brine. The refractive index of the lens is less than that of the surrounding medium and the focal length is negative! An erect diminished virtual image of the face is seen in the concave lens.
2 A rubber ball has a figure inside. The ball acts as a single surface magnifying lens.
Dropping the ball into water reduces the refractive index difference at the front surface reducing both the focal length and the magnification.
3 Images of the Buddha
ISB is an International School in the Kingdom of Thailand, a beautiful country with a Buddhist society. The image of the Buddha permeates the land and molds the spirit of its people.
A hollow marble is held between the camera and the image. Two images appear. The larger outer image is inverted and a little out of focus. The smaller sharper, inner image, is upright.
Questions
*1 Account for the budha images in the marble (Example 3). Locate them, and describe their size and orientation by applying the lens formula or by some other method.
*2 Two lenses are shown above two different pages. Assuming that the images are formed at the near point of the eye (20 cm) and the magnification is optimal, determine the power and focal length of the lenses.