Daniel Chang: 2005
|
Any freely falling object reaches terminal velocity when the drag force equals the weight minus the buoyancy force, and no further acceleration takes place.  |
Research Question
What is the relationship between the radius of a ball and the
terminal velocity when falling in water?
Hypothesis
The terminal velocity vT will be proportional to r2 and to the difference in the densities of the material and the fluid (in this case water).
Explanation
At low speeds, in the laminar flow region, the terminal velocity
of a ball falling in a fluid is related to Stokes' law1.
The drag force equation is ...
... where r is the radius of the sphere, h (eta) is the viscosity, and v is the velocity. Substituting in the equation above, at terminal velovcity....
... where r1 and r2 are the densities of the sphere and the fluid respectively, and h is the viscosity of the fluid.
The terminal velocity is given by....
It is assumed that since the velocities are low, Stokes' law will apply. At higher speeds, in the turbulent flow region, drag is proportional to velocity squared and the terminal velocity is then proportional to the square root of the radius.
Materials & Procedure
Sandpaper was used to roughen the surface of a plastic tube (shown at right) and a plastic top before applying silicon sealant between the top and the tube. Another layer of silicon sealant was added around the plastic top where it met the tube. The sealant was left to dry overnight. The tube leaked on the first attempt. On the second attempt the seal held.
Seven steel balls and five glass balls were used in this experiment. The mass of each ball was found with an electronic balance and vernier calipers were used to measure the diameter of each ball.
A bucket was placed under the water filled tube in case of leakages. Two 500 Watt halogen lamps were used and a digital video camera was positioned on a tripod as shown. A rubber band secured a meter stick to the plastic tube.
The film was analyzed frame by frame. Displacement-time data was used to find the terminal velocity in each case and graphs were plotted in Logger Pro showing terminal velocity against radius and mass for each material.
Terminal velocity
The tube (figure 1) was one meter deep. Dropping balls were filmed and the fim was exported as jpg images.
Graph 1 is a composite image compiled from strips of equal width taken from successive frames of the movie clip for the largest steel ball falling in the water. It clearly shows that terminal velocity is approached very nearly after a fall of 50 cm. Terminal velocity is reached before this level for the smaller steel spheres and for the glass marbles which are of lower density. The terminal velocities listed in Table 1 below, were measured in the lower half of the tube by measuring the time taken for the ball to travel 15 cm. Two meaurements were made for each ball in different parts of the tube. The errors listed in Table 1 for the terminal velocities were obtained by taking half the range.
Note: the tube was relatively narrow and the balls slowed a little when near the walls. This 'wall effect' will be investigated at a later date. For these measurements the effect contributed to the errors in terminal velocity lised in Table 1.
Table 1a lists the ratios of the terminal velocity of the steel balls and the density of the steel balls compared to the terminal velocity of the glass balls and the density of the glass balls with similar radius.
The approach to terminal velocity
In Graph 1 the line appears to be straight within errors in the upper right quadrant, but the velocity-time graph is asymptotic to the terminal velocity. Distance-time data read directly from Graph 1 is listed in Table 2.
Table 2
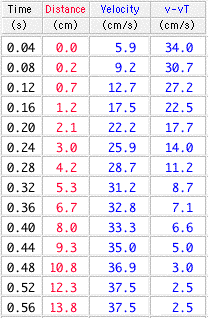
Graph 2 shows the approach to terminal veocity. The graph has been prepared in Logger Pro by differentiating the distance data with respect to time. The data is a good fit to an exponential function.
Terminal velocity versus ball radius
The velocity was measured twice in different parts of the lower half of the tube by dividing the distance traveled by the time. The two distances were in each case the same to within ±1 mm on the screen. The 5 cm markings on the ruler were used to scale the measured distances to find the displacement in meters. The average of the measured velocities was taken to be the terminal velocity. The possible errors are listed in Table 1.
The terminal velocity is plotted against the radius of the balls in Graph 3. The error bars show maximum and minimum values listed the table 1 for the terminal velocity. A power law function has been fitted to both data sets to find the relationship between the radius of the ball and its terminal velocity in water.
The power is the same within errors for each material: very close to 0.50.
Graph 4 shows the terminal velocity plotted against the square root of the radius. Graphs 3 and 4 clearly show that, within errors, the terminal velocity is proportional not to the square of the radius but to the square root. Stokes' law, which applies under conditions of laminar flow, does not apply in this case. The balls are falling in turbulent flow.
The density of each individual ball was calculated by dividing mass by the volume, calculated by using the radius, measured with a vernier caliper. Table 1a shows the ratios of the terminal velocity and the density of the steel and glass balls. The density of the glass balls varied a little which adds additional errors.
The terminal velocity is, within errors, proportional to the square root of the ball radius and depends on the density. The ratio of the terminal velocities for steel and glass is approximately 2.0. Stokes' law does not apply in this situation because if it did the terminal velocity would be proportional to the radius squared.
During the preparation of this paper it has been shown by Baker and Keys(2) that the the drag force for metal cups falling in water is proportional to velocity squared by finding the terminal velocities of cups of different masses. In this situation turbulence is present and the drag force is given as a first approximation by the relationship....
... where r2 is the density of the water, A is the cross sectional area of the sphere (pr2) and v is the velocity.
Putting the drag force equal to the weight minus the buoyancy force gives....
At once, the terminal velocity is proportional to the square root of the radius and the ratio of terminal velocities is given by ...
The dependence of terminal velocity on the square root of the radius has been confirmed within errors for both steel and glass balls. The right hand side of the equation above is given by the square root of 6.66/1.56 which is 2.10. For the 4.75 mm radius steel and glass balls the ratio of terminal velocities from Table 1 is given by ...
vs/vg = (1.36±0.1)/(0.68±0.1) = 2.0 ± 0.1
The result in this single case is consistent (within errors) with the predicted dependence on ball density. More measurements are required to confirm the relationship over a range of radii.
Errors
The densities of the steel and glass balls were both found to vary by as much as 5%. When related measurements are repeated, balls of the same density should be found.
When the balls moved close to the walls of the contained the terminal velocity reduced by 5-10%. If a tank with a larger diameter was available more consistent data could be obtained.
The gradual approach to terminal velocity is shown in Graphs 1 and 2. The velocities measured in the lower half of the one meter deep tank were close to, but not exactly, terminal velocities. A deeper tank would give more accurate estimates of the terminal velocities.
Suggestions For Further Work
Balls of the same radius but of different masses could be used
to plot the dependence of terminal velocity on ball density. Graph 5 shows mass
plotted against velocity squared for two points (the steel and
glass balls of 4.75 mm radius. The interecept is the mass of water
displaced. The value (0.4 g) is close to the expected value (0.44
g). Two points are not sufficient to establish the relationship
between mass and velocity squared, but the intercept is close
to the expected value.
Water (or other liquids and solutions) could be used to plot the
dependence of terminal velocity on the viscosity of the liquid
which is a function of temperature.
If dye was placed in narrow layers in a column of water, a film of a falling steel ball would confirm that turbulence occurs and Stokes' law does not apply. A suspension of plastic chips in water may be equally effective.
References
1 http://www.answers.com/topic/stokes-law
2Baker and Keys 2006: Terminal velocity
in water and oil
3 http://www.engineeringtoolbox.com