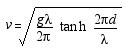
Jacobs .... with the class of 2006
Abstract
The velocity of ripples is measured in a shallow tank which was rocked back and forth. The velocity-depth relationship in this special case is found to be a power law with an exponent of 0.28 ± 0.2.
Ocean swells, and breaking waves close to the shoreline, disturb the sand on the sea bed if the wave amplitude is above 10-20% of the water depth. For this reason, shells and other things, are washed up during storms. An Applet on the web (1) is set to calculate under-water motion for different conditions.
In shallow water, the elliptical paths followed by water 'particles' below a passing gravity wave, flatten to horizontal lines, particularly at the bottom, where no vertical flow is possible. The interaction with the bottom slows the wave velocity increasingly as the depth is reduced. It can be shown that in large bodies of water, shallow-water gravity waves, with wavelengths very much greater than the water depth (10-20 times), have a wave speed that is related to the depth (2).
The general expression for the speed of surface gravity waves....
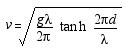
... becomes....
The expression is not well known in non specialist circles. One writer on the web, in answer to a question, states that the wave speed is proportional to the depth (3).
Research question
Is a square root power law a good approximation to the velocity-depth relationship for ripples of ~1-2 cm wavelength in a shallow flat bottomed tank for depths between 1 mm and 1 cm?
Hypothesis
Ripples are normally regarded as capillary waves with restoring forces provided at least in part by surface tension. Detergent is added to the water for these measurements which is expectd to lower the surface tension. Sato (4) showed in a preliminary set of measurements that increasing the level of detergent did not affect the ripple velocity. For this reason the ripples in this case are tentatively regarded as gravity waves and are therefore expected to behave in similar ways to large scale ocean waves. If the water can be redgarded as shallow the velocity will be proportional to the square root of the depth.
Explanation
Since the wavelength of ripples is greater than one cm, the depth of water in the tank is less than the wavelength. At least to a first approximation, the behavior of ripples in the tank under these conditions is expected to be similar to the behavior of shallow-water waves in large bodies of water, provided they can be regarded as gravity waves. .
A shallow flat bottomed aluminum tank (30x30x3 cm) was purchased. It was important to ensure that the bottom was accurately flat so that the depth of water was uniform. The tank was placed on a level table. Since tap water does not wet the bottom at depths below about 3 mm a little detergent was added to the water. [Aya Sato: 2003, (private communication) measured ripple velocity in a similar tank using digital movie clips. She found the velocity to be independent of the concentration of detergent.] A one millimeter deep layer of water will now wet the bottom of the tank.
The precautions, ensuring the tank was flat, and adding detergent ensured that the water depth, and hence the wave speed were controlled.
Because water has a meniscus it is not possible to measure the water depth with a ruler. The depth (D) was therefore inferred by adding 90 ml of water each time to the 30x30 cm tank.
The tank was carefully leveled so that ripples remained straight as they crossed the tank. The tank was placed on two rulers so that it could be rocked to reflect ('throw') a ripple repeatedly back and forth. In this way, a longer path length (150 cm) was achieved and a more accurate time could be measured with a stop watch. The method required some practice, and introduced additional errors which probably lead to a slight over estimate of the time required.
The measurements were completed by eight groups of two students. Each time measurement was repeated three times and the average value was recorded.
The tank was rocked and the times for five passes of the ripples were measured with a stop watch. Particular care was taken to ensure that accurate data was obtained for the shallow depths (1 and 2 mm). The averages of the eight readings are listed in table 1 with the standard deviation used as the error in each case.
Table 1
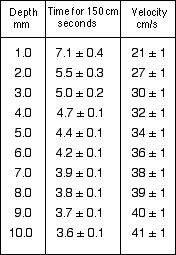
The velocities are accurate to within ±1 cm/s.
The data is plotted in Graph 1. The error bars on the graph are comparable in size to the point protectors and have not been plotted separately. The data points follow a smooth curve which is a good approximation to a power law with an exponent of 0.28.
Graph 1a shows two manual power laws fitted to the data within errors. The exponent in the power law of best fit (Graph 1) has been determined to within ±10% as....
Graph 2 shows the power law of best fit and a second power law with exponent 0.5. Clearly, the wave velocity under these conditions, follows a power law, but is not proportional to the square root of the depth.
Discussion
The refraction of water waves in a shallow ripple tank is a standard introductory physics demonstration that is done in every high school physics classroom. The normal demonstration of changing wave speed with depth is done by tipping the tank. The exact relationship between wave speed and depth for shallow water waves is not part of the IB curriculum, but the topic is accessible experimentally at this level. The non compliance of these measurements with the predicted square root dependence could be a consequence of the method used (rocking the tank creates two regions of different depths) or it could show that the predicted relationship does not hold for these ripples in very shallow water. The latter explanation is the more likely since the wavelength is not 20 times the depth - the condition for the shallow wave equations to hold.
There are several additional sets of measurements which could be made, with relatively simple apparatus.
1 Ripples radiating from a point source could be filmed with a digital camera and the velocity found in this way. Because there is very little reflection from the water surface at normal incidence a glass bottomed tank could be used in sunlight and the patterns formed on white paper below the tank could be filmed. The sun is an excellent source of bright parallel light . The sun is overhead at mid-day in Bangkok
2 A rectangular glass tank (200x50x10 cm) could be placed on a table. Since the width of the tank (50 cm) would be more than ten times the depth of the water the effect of the edges would be small. If the tank were leveled and partly filled with brine of just the right density to suspend plastic chips, the following measurements could be made.
a The plastic chips in the center of the tank could filmed with a digital video camera (with very limited depth of field) as waves of different amplitude passed down the tank. The film could be examined to trace the actual water movement as a function of depth and wave height.
b The dispersion of a pulse could be mapped in the same way.
c The long shallow tank could be elevated at one end by tipping the table and the profile of the waves could be photographed as they passed from deep to shallow water. The velocity-depth relationship could be plotted for water depths of 6 cm to zero with waves of 1-4 cm initial amplitude.
Evaluation
The method used here (rocking the tank) produced consistent measurements with relatively small standard deviations but conditions in the rocking tank were not exactly the same as they would be in a stationary tank. Especially at very shallow depths, the ripple was more like the advancing edge of a deeper layer of water than a single pulse, gravity-wave, in the normal sense. The deviation found in the exponent of the power law from that predicted for shallow water waves may be accounted for by this difference but there is an additional complicating factor.
The tank is correctly described as a "shallow water tank" but the ripples are of relatively short wavelength. Since waves are classified as "deep-water" when the depth is greater than half the wavelength, at best the ripples in the shallow water tank are intermediate waves, not "shallow-water" waves.
Further work is required before definitive statements could be made.
References
1 Dalrymple R. 2002: http://www.coastal.udel.edu/faculty/
3 Jones D. 2002: http://ww.mcaso.com/qa_wws.html
4 Aya Sato: ISB 2003. Aya filmed waves in a ripple tank with a digital camera, and showed that the velocity was independent of the concentration of detergent. Private communication.
Editor's comments
1 The IB style write-up has at least one minor weakness. IB examiners prefer to see a separate section discussing the selection and control of variables. In research reports, comments of this nature are included in a general introduction.
2 Very short wavelength, high frequency, surface water waves, are known as capillary waves. The restoring force, and consequently the velocity, depends - at least in part - on surface tension. This possibility was discounted because an attempt was made by another student in this laboratory to change the ripple velocity by increasing the concentration of detergent. The negative result of that test is taken to indicate that the ripples are gravity waves.
To continue with this investigation a wave-speed calculator will be used to predict the velocity of ripples of varying wavelengths generated with a vibrator in the tank, with and without considering the surface tension.
Ed.