Introduction
When light passes from one uniform medium to another the ratio sin i over sin r (where the angles have their usual definitions) is a constant. The relationship is known as Snell's law. Willebrord Snell is credited with its discovery in 1621. As is common in the history in science the truth is a little more complex. Thomas Harriot was aware of the relationship in 1602, having made measurements in 1597-98(1). Like Snell his results remained unpublished in his lifetime. Prior claim could be made for Ibn Sahl (also known as Ibn-al-Haitham) who wrote of his deternination of the shape of an aspherical lens that will focus light without distortions in 984, but Ibn's account was of a geometrical construction rather than actual measurements. In France, Snell's law is often called "la loi de Descartes" since René Descartes independently derived the law in terms of sines in his 1637 treatise Discourse on Method, and used it to solve a range of optical problems(2).
In this exercise, angles of incidence and refraction are measured on photographs. Snell's law is not in doubt. What is in doubt is the level of distortion in the photographs the consequent accuracy of the measurements.
Procedure
A beam of red light from a laser pointer was shone through a square 10x10 cm perspex block placed on white paper. The beam was visible as it entered and left the block (figure 1). The angle of incidence was varied from zero to 80 degrees and the block and beam was photographed from a point 50 cm directly above the center of the block. The side shifted ray emerged parallel to the incident ray to within ± 0.5° (see figure 1).
 Fig 1 An inverted photograph of a red laser beam passing through a perspex block. The beam enters from the left and exits at right. The emerging ray appears to be side-shifted and to be parallel to the incident ray to within half a degree. |
Data
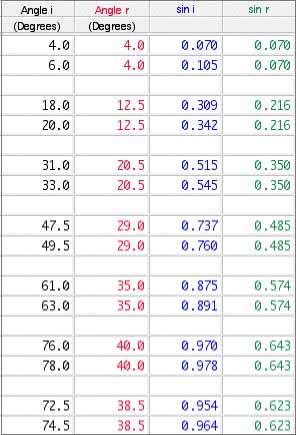
The angles of incidence and refraction were measured with a protractor on photographs printed actual size. The values are listed in table 1. The table entries are the average of two measurements, one entering and one leaving the block. Possible maximum and minimum values are shown, representing the estimated error of ±1° for angle i. The calculated values of sin i and sin r are listed also with possible maximum and minimum values.
Table 1
Analysis
Graph 1 shows the angle of incidence plotted against the angle of refraction. The maximum and minimum points are plotted with point protectors in the form of an open cross to represent the error bars. The data is sufficiently accurate to show that the graph is not linear.
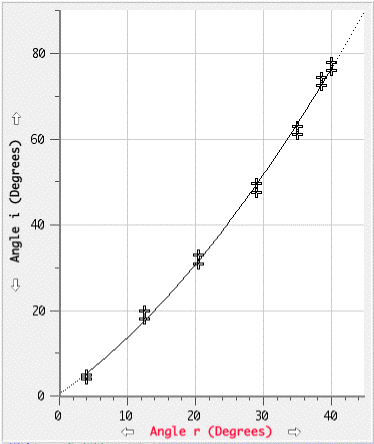
Graph 1 An arbitrary curve has been fitted to the points to show that the relationship between angle i and angle r is not linear.
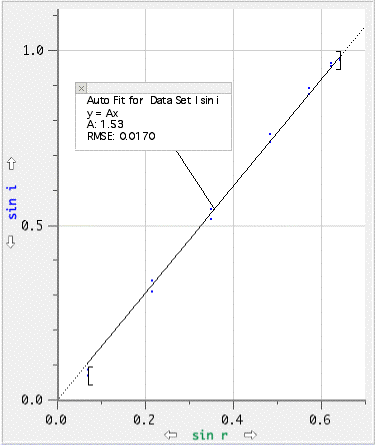
Graph 2 shows sin i plotted against sin r. Sin i is proportional to sin r since the line of best fit is straight, and passes through the origin.
Graph 2 A straight line passing through the origin has been fitted to the points to show that the relationship between sin i and sin r is linear.
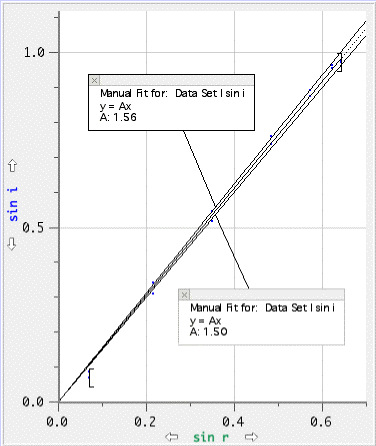
Possible maximum and minimum points calculated in Logger Pro are shown on the graph. The slope of the line of best fit (the refractive index of perspex w.r.t. air) is 1.53. Graph 3 shows possible extreme lines.
Graph 3 Extreme lines have been fitted within errors to show the possible error inthe slope n.
The refractive index n is the slope of the straight line ...
n = 1.53 ± 0.03 The refractive index is close to that of glass, (1.50).
Discussion
Drawing around the perspex block with a pen and marking the incident and refracted rays on paper produced a sin i versus sin r graph that was straight within errors, and gave a slope of 1.5, but the data was not sufficiently accurate to show that the angle i - angle r graph was not a straight line. The difference between the angle i - angle r graph and the sin i - sin r graph is clearly demonstrated by these measurements.
Logger Pro will not plot a sin i = 1.5 sin r curve. The curve fit on graph 1 is a quadratic function. It is presented to show only that the relationship is not linear.
References
(1)http://en.wikipedia.org/wiki/Snell%27s_law
(2)http://mintaka.sdsu.edu/GF/explain/optics/discovery.html