An impulse is a kick in street language. A ball is kicked suddenly, by large force acting for a very short time. Impulse, in Newton seconds, is defined as the area under the force-time graph.
|
When the well known equation that describes the acceleration of a mass under the influence of a constant unbalanced force (f = ma) is writen in terms of the definition of constant acceleration (Dv/t), two expressions arise. The quantity f.t, which is defined as impulse and mv which is defined as momentum. |
A block of mass m, slides on a flat uniform rough surface. Friction is a constant retarding force. The block has a constant negative acceleration. The velocity-time graph as the block is coming to rest is a straight line. The slope of the line a is Dv/t.
Remembering that ...
F = ma. Gives at once ...
... where F is the constant friction force.
Rearranging gives....
The impulse F.t is equal to the change in momentum.(mv - mu).
Note: the math above is true for any constant force. It can be shown that the result holds when the force is not constant.
|
Suppose that for the sliding block at right, the change in velocity is 1.50 m/s. The mass is 1.07 kg. The friction force is - 2.28 N acting for 0.7 seconds.
|
When the net force is not constant (eg. a varying applied force minus a friction force) the relationship between impulse and momentum-change still holds.
A 24.5 kg drum of water on a cart is pushed with a force probe under carefully controlled conditions. The velocity time graph is a straight line since the friction force is constant and the floor is flat. The constant negative acceleration is -0.26 m/s/s.
The constant friction force is - 6.4_Newtons since....
The unbalanced accelerating force is the measured force, minus the constant friction force. The net impulse applied to the drum is the area under the force-time graph at right where the calculated friction force has been subtracted from the measured force in Logger Pro.
The momentum gained by the drum is mv.
The momentum gained in this instance is equal to the net impulse, (within errors). Repeating the demonstration ten times (five from each side of the room) gave the collected data listed in table 1.
Table 1
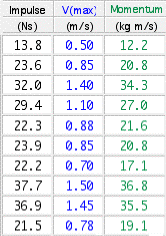
The data lisrted in table 1 is accurate to within ±5%.
A plot of applied-impulse versus momentum-gained is shown in graph 3. The line is straight, with a slope of 1.0 within errors, as expected.
In any explosion, the energy input becomes heat and kinetic energy, and momentum is conserved. A simple situation is the classic blacksmith's anvil shoot, popular in Colonial US times, as a July the fourth celebration. For entertainment, they took two anvils, turned one over on top of the other, and filled the hollow with black powder.
| Gene Purcell is pouring gun powder into the cavity in the bottom anvil, in preparation for the shooting of the top anvil. |
 |
They stood back, and lit the powder. The ground shaking explosion could be heard for 15 miles. It threw the top anvil 50 meters into the air above the tree tops, and half buried the bottom one in the ground (equal and opposite impulses). Next year, they did it again!
The bottle rocket shown is fueled with an explosive 2:1 mixture of hydrogen and oxygen (the most energetic reaction per gram known). The remaining water acts as a plug, but more importantly, acts as mass that is expelled at high speed. The total momentum is conserved - remaining zero after ignition. The presence of the water imparts greater forward momentum to the now empty plastic bottle. A rocket is a reaction engine.
|
|
> More difficult questions |